Equiscomponibilita' fra triangolo e trapezio un trapezio e' equivalente ad un triangolo avente come base la somma delle basi e come altezza la stessa altezza Consideriamo il trapezio ABCD ed il triangolo ABE 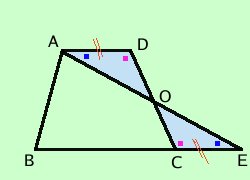ipotesi AD = CE tesi ABCD equivalente ABE Considero i triangoli AOD ed OCE essi hanno: AD = CE per ipotesi DAO^= OEC^ perche' angoli alterni interni rispettoalle rette parallele AD e CE tagliate dalla trasversale AE ADO^= OCE^ perche' angoli alterni interni rispettoalle rette parallele AD e CE tagliate dalla trasversale DC Quindi i due triangoli AOD ed OCE sono congruenti per il secondo criterio di congruenza. Considero ora la figura ABCO: aggiungendo alla figura ABCO il triangolo ADO si ottiene il trapezio ABCD di partenza aggiungendo alla figura ABCO il triancolo OCE si ottiene il triangolo ABE di partenza Le due figure ABCD ed ABE sono equicomposte e quindi equivalenti (equiestese) come volevamo