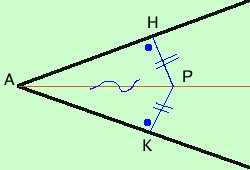
Punto equidistante dai lati dell'angolo --------> Punto appartenente alla retta che divide l'angolo in due parti congruenti Come ipotesi abbiamo che il punto ha la stessa distanza dai lati dell'angolo; dobbiamo dimostrare che il punto allora si trova sulla retta che divide l'angolo in due parti congruenti. ipotesi    PH = PK    PHA^= PKA^= angolo retto    tesi    PAH^= PAK^    Dimostrazione considero i due triangoli rettangoli PAH e PAK; essi hanno: PH = PK per ipotesi il lato PA in comune Quindi i due triangoli sono congruenti per uno dei criteri di congruenza dei triangoli rettangoli e quindi hanno congruenti tutti gli elementi, in particolare PAH^= PAK^ come volevamo