Punto appartenente alla retta che divide l'angolo in due parti congruenti --------> Punto equidistante dai lati dell'angolo Come ipotesi abbiamo che il punto si trova sulla retta che divide a meta' l'angolo; dobbiamo dimostrare che il punto allora ha la stessa distanza dagli estremi del segmento. ipotesi    PAH^= PAK^    tesi    PH = PK    Dimostrazione Dal punto P traccio le perpendicolari PH e PK alle rette r ed s A Se il punto P e' il punto medio del segmento allora ha la stessa distanza dagli estremi del segmento e considero i due triangoli rettangoli PAH e PAK; essi hanno: 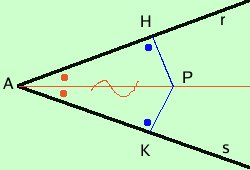PAH^= PAK^per ipotesi il lato PA in comune Quindi i due triangoli sono congruenti per uno dei criteri di congruenza dei triangoli rettangoli e quindi hanno congruenti tutti gli elementi, in particolare PH = PK come volevamo