Terzo criterio di congruenza fra triangoli Due triangoli sono congruenti se hanno tutti e tre i lati congruenti Per la dimostrazione mettiamo il problema nella forma se... allora... (quello dopo il se e' l'ipotesi e quello dopo l'allora e' la tesi) Se due triangoli hanno congruenti i tre lati allora i triangoli sono congruenti Scriviamolo in modo geometrico: ipotesi, tesi e figura corrispondente 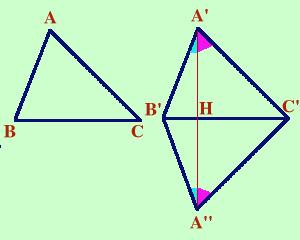Ipotesi AB = A'B' BC = B'C' CA = C'A' tesi ABC=A'B'C' Dimostrazione: Trasporto il triangolo ABC da banda opposta rispetto al triangolo A'B'C' in modo che il lato BC vada sopra il lato B'C'; allora il punto A va in A''. Considero il triangolo A'B'A'': esso ha due lati uguali (A'B'=A''B') quindi ha anche due angoli uguali cioe' B'A'H=B'A''H (quelli indicati in azzurro) Considero ora il triangolo A'C'A'': esso ha due lati uguali (A'C'=A''C') quindi ha anche due angoli uguali cioe' C'A'H=C'A''H (quelli indicati in viola) Considero ora i triangoli A'B'C' ed A''B'C' essi hanno: A'B' = A''B' per ipotesi (ho fatto fare un movimento rigido a due lati uguali per ipotesi) A'C' = A''C' sempre per ipotesi (come sopra) Gli angoli B'A'C'=B'A''C' sono uguali perche' somme di angoli uguali (quelli colorati) Quindi i due triangoli sono uguali per il primo criterio come volevamo dimostrare. 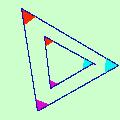Il terzo criterio fa riferimento a tre lati uguali; Potremmo dire che due triangoli sono uguali se hanno uguali tre elementi, pero' cio' non vale per i tre angoli: a destra puoi vedere un esempio che ti mostra due triangoli con i tre angoli uguali ma che non sono uguali. In matematica per mostrare che una proprieta' non e' vera basta far vedere un esempio che mostri che non e' verificata