Primo criterio di congruenza fra triangoli Due triangoli sono congruenti se hanno congruenti due lati e l'angolo compreso Per la dimostrazione mettiamo il problema nella forma se... allora... (quello dopo il se e' l'ipotesi e quello dopo l'allora e' la tesi) Se due triangoli hanno congruenti due lati e l'angolo compreso allora i triangoli sono congruenti Scriviamolo in modo geometrico: ipotesi, tesi e figura corrispondente Ipotesi 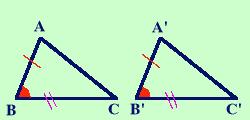AB=A'B' BC=B'C' ^ ^ A B C = A' B' C' tesi ABC=A'B'C' Dimostrazione: Trasporto l'angolo B sopra l'angolo B' (posso farlo perche' sono congruenti per ipotesi e potrei farlo in due modi diversi: o facendo scivolare l'angolo o ribaltandolo; devo dire che lo porto sopra senza ribaltarlo) in modo che il lato AB vada sopra il lato A'B' ed il lato BC vada sopra B'C'; in questo modo i due triangoli hanno A su A', B su B' e C su C' quindi sono sovrapposti e coincidono punto per punto C.V.D. (Come Volevamo Dimostrare) Quando ero studente io si era piu' esigenti e si diceva C.D.D. cioe' Come Dovevasi Dimostrare ed in qualche testo c'era addirittura Q.E.D. Quod Erat Demonstrandum che e' la stessa cosa in latino Da notare che per la dimostrazione parto dall'elemento in mezzo agli altri due