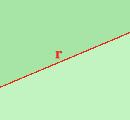
Angoli Considero una retta r su un piano: il piano viene diviso in due parti che chiamero' semipiani di origine la retta r Per ogni cosa nuova che trovo devo prima di tutto controllare la congruenza: posso aggiungere ai postulati che tutti i semipiani sono tra loro congruenti 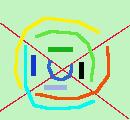Considero due rette sul piano: ottengo troppe cose: ad ogni colore corrisponde una figura e ne ho segnate solo alcune allora considero due semirette aventi la stessa origine: ottengo che il piano viene diviso in due parti che chiamero' angoli 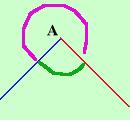: per darne la definizione basta dire come l'ho trovato: Definizione: L'angolo e' una delle due parti in cui il piano viene suddiviso da due semirette aventi la stessa origine Per tutti gli enti geometrici che troveremo dovremo parlare di congruenza, diseguaglianze e delle operazioni che su questi enti posso applicare: sugli angoli dovro' considerare: congruenza somma differenza Inoltre il concetto di angolo ci porta ad un nuovo concetto: la convessita' 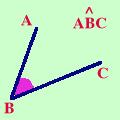Per indicare un angolo scriveremo tre lettere: la prima posta su un lato, la seconda nel vertice dell'angolo e la terza sull'altro lato mettendo il simbolo di angolo sopra la lettera al centro e preferibilmente cercheremo di seguire un verso antiorario nella lettura delle lettere