esercizio Date le parabole y= x2 + 2x - 2 e y= -x2 + 6x - 4 verificare che sono tangenti nel loro punto comune Soluzione: 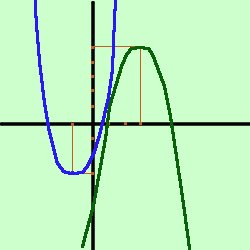Intanto disegniamo le due parabole Due parabole sono tangenti fra loro se hanno la stessa tangente nel punto comune, quindi prima trovo il punto comune, poi calcolo la tangente in questo punto per oguna delle due parabole e controllo che siano identiche Faccio il sistema fra le due parabole y = x2 + 2x - 2 y= -x2 + 6x - 4 Sostituisco il valore della y dalla prima equazione nella seconda ed ottengo y = x2 + 2x - 2 x2 + 2x - 2 = -x2 + 6x + 4 ---------------- 2x2 - 4x + 2 = 0 Divido tutti i termini per 2 ---------------- x2 - 2x + 1 = 0 ---------------- (x-1)2 = 0 y = (1)2 + 2(1) -2 x = 1 (soluzione doppia) y = 1 x = 1 (soluzione doppia) Quindi abbiamo il punto comune A(1;1) Calcoliamo adesso le tangenti alle parabole nel punto A tangente in A alla prima parabola y=x2 + 2x - 2 fascio di rette in A: y-1 = m(x-1) y = mx - m +1 faccio il sistema poi metto il delta uguale a zero y = x2 + 2x -2 y = mx - m +1 Sostituisco y = x2 + 2x -2 x2 + 2x -2 = mx - m +1 ----------------------------- x2 + (2-m)x -3+m = 0 pongo il delta dell'equazione uguale a zero = b2-4ac = 0 Ho a = 1       b = 2-m       c = -3+m = b2-4ac = (2-m)2 - 4 (1)(-3+m) =0 4 - 4m + m2 + 12 -4m =0 m2 -8m + 16 =0 (m-4)2 = 0 m = 4 quindi abbiamo la tangente 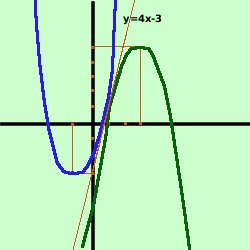y -1 = 4(x-1) y = 4x - 3 tangente in A alla seconda parabola y= -x2 + 6x - 4 fascio di rette in A: y-1 = m(x-1) y = mx - m +1 faccio il sistema poi metto il delta uguale a zero y = -x2 + 6x - 4 y = mx - m +1 Sostituisco mx - m +1 = -x2 + 6x - 4 y = mx - m +1 x2 + (m-6)x + 5-m = 0 ------------------- pongo il delta dell'equazione uguale a zero = b2-4ac = 0 Ho a = 1       b = m-6       c = 5-m = b2-4ac = (m-6)2 - 4 (1)(5-m) =0 m2 - 12m + 36 - 20 + 4m =0 m2 -8m + 16 =0 (m-4)2 = 0 m = 4 quindi, anche qui abbiamo la tangente y -1 = 4(x-1) y = 4x - 3 Essendo le tangenti identiche le due parabole sono tangenti fra loro, come volevamo