Disegniamo la parabola di equazione
y= x2
- 6x + 5
Troviamo prima le coordinate del vertice V
| V= (
|
b
-  ; ;
2a
|
b2-4ac
-  ) )
4a
|
abbiamo
a = 1
b = -6
c = 5
quindi
| V= (
|
-6
-  ; ;
2·1
|
(-6)2-4·1·5
-  ) )
4·1
|
| V= (
|
3
|
16
-  ) )
4
|
Intersezioni con gli assi
- Intersezioni asse x: faccio il sistema fra l'asse x (y=0) e
l'equazione della parabola
 y = 0
y = 0
y= x2
- 6x + 5
 y = 0
y = 0
x2
- 6x + 5 = 0
risolvo l'equazione di secondo
grado ed ottengo
x1 = 1
x2 = 5
quindi i punti di intersezione con l'asse delle x sono
(1,0) (5,0)
- Intersezioni asse y: faccio il sistema fra l'asse y (x=0) e
l'equazione della parabola
 x = 0
x = 0
y= x2
- 6x + 5
 x = 0
x = 0
y = 02 - 6(0) + 5 = 5
quindi il punto di intersezione con l'asse delle y e'
(0,5)
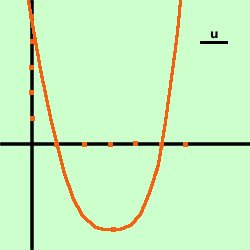
Adesso congiungo i punti con una curva continua ed ottengo il grafico della
parabola
|

