Distanza di un punto da una retta E' un problema che potrebbe essere risolto con le nozioni che gia' abbiamo: basta fare perpendicolare dal punto alla retta intersezione fra la retta e la perpendicolare, trovo il piede della perpendicolare Distanza fra il punto ed il piede della perpendicolare Pero' e' usata tanto spesso che merita una formula a se' stante, do solamente la formula finale, se vuoi dimostrarla devi fare il procedimento indicato sopra per la retta generica ed il punto P(x0,y0) Distanza del punto P(x0,y0) dalla retta y = mx + q formula          y0 - mx0 - q d = ----------------------             (1 + m2) Essendo la distanza sempre positiva se sopra e' piu' sotto scegli il piu', se sopra hai meno sotto prendi meno. In questo modo il risultato sara' sempre positivo Facciamolo anche per la retta in forma implicita Distanza del punto P(x0,y0) dalla retta ax + by + c = 0 formula          ax0 + by0 + c d = ----------------------             (a2 + b2) Anche qui se sopra e' piu' sotto scegli il piu', se sopra hai meno sotto prendi meno. In questo modo il risultato sara' sempre positivo Esempio: trovare la distanza fra la retta y = -x - 2 ed il punto P(0,4) Applico la formula:          y0 - mx0 - q d = ----------------------             (1 + m2) sapendo che 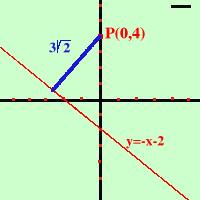x0 = 0 y0 = 4 m = -1 q = -2          4 - (-1)·0 - (-2) d = ----------------------             [1 + (-1)2)]         6 d = ------- = 32      + 2 Un po' piu' di 4 unita' di misura come puoi controllare dalla figura