Retta per l'origine Consideriamo dei punti allineati con l'origine degli assi: A1 = (x1, y1)    A2 = (x2, y2)    A3 = (x3, y3)    ........... I puntini stanno ad indicare che posso prendere quanti punti voglio. Al solito posizioniamo i punti nel primo quadrante, il risultato sara' comunque valido in tutto il piano 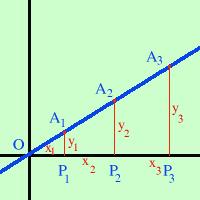Dai punti A1 A2 A3 mando le perpendicolari sull'asse x e trovo i punti P1 P2 P3 so che: OP1 = x1 OP2 = x2 OP3 = x3 inoltre A1P1 = y1  A2P2 = y2  A3P3 = y3 Cosa notiamo? Essendo i punti allineati i triangoli OA1P1, OA2P2, OA3P3 sono simili quindi posso fare la proporzione A1 P1      A2 P2      A3 P3      -------- = -------- = --------  O P1       O P2       O P3      e questo vale per tutti i punti che sono allineati Se il rapporto lo chiamo m A1 P1      A2 P2      A3 P3      -------- = -------- = -------- = m  O P1       O P2       O P3      allora per tutti i punti allineati potro' dire che il rapporto fra la coordinata verticale e quella orizzontale sara' m y1     y2     y3 --- = --- = ---- = m x1     x2     x3 Preso un punto generico P(x,y) esso sara' allineato se y --- = m x cioe' sviluppando     y = mx y = mx sara' quindi l'equazione della retta passante per l'origine In particolare porremo per l'asse delle x l'equazione y = 0 per l'asse delle y l'equazione x = 0 L'equazione y = 0 corrisponde al valore m = 0 mentre esiste una retta che corrisponde ad un valore di m che non esiste: il valore infinito; a questa retta (asse y) assegniamo l'equazione x = 0 Vista l'importanza dell'argomento approfondiamo un po' Come si disegna la retta per l'origine Significato di m Come si determina m