Il sistema di coordinate cartesiane ortogonali nel piano in pratica dobbiamo riprendere il sistema come fatto sulla retta e lo applichiamo su due rette perpendicolari 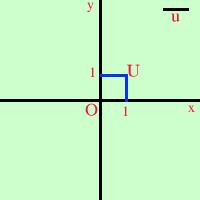Consideriamo un piano e, su di esso, due rette fra loro perpendicolari e un'unita' di misura u Indichiamo come punto O (origine) il punto di incontro delle rette e ad esso assegniamo la coppia di valori (0,0) Sulla retta orizzontale fisso il punto 1 ottenuto riportando a destra di O l'unita' di misura. Sulla retta verticale fisso il punto 1 ottenuto riportando in alto rispetto ad O l'unita' di misura. Dal primo punto ottenuto mando la verticale e dal secondo l'orizzontale; chiamo U (unita') o punto (1,1) il punto ottenuto. In questo modo ottengo una corrispondenza biunivoca fra i punti del piano e le coppie ordinate di numeri reali, nel senso che ad ogni coppia di numeri corrisponde un punto nel piano e ad ogni punto nel piano corrisponde una coppia di numeri reali. Indicheremo con x o asse delle ascisse la retta orizzontale indicheremo invece con y o asse delle ordinate la retta verticale Studiamo il sistema nei particolari Vediamo ora alcuni casi particolari poco usuali sistemi di coordinate cartesiane non ortogonali sistemi bimetrici