Soluzione del problema Siccome parlare di aree negative e' in matematica quasi una bestemmia dovremo vedere come rendere sempre positivi i valori delle aree: 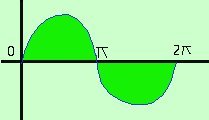Dovremo considerare con segno positivo gli integrali calcolati su aree sopra l'asse x e considerare invece con segno cambiato (negativo) gli integrali calcolati su aree sotto l'asse delle x Quindi considerando che da zero a pigreco siamo sopra l'asse x e che da pigreco a due pigreco siamo sotto, per calcolare l'area cercata dovremo scrivere: sen x dx - sen x dx = = - cos x - - cos x = = - cos + cos 0 - (-cos 2 + cos ) = = - cos + cos 0 + cos 2 - cos = = -(-1) + 1 + 1 - (-1) = = 1 + 1 + 1 + 1 = 4 l'area cercata e' di 4 unita' quadrate del piano La figura ha unita' diverse in orizzontale e verticale perche' pigreco vale 3,14 e il seno in altezza varia da 1 a -1, quindi i quadratini unitari sarebbero dei rettangolini