|
Per calcolare l'integrale definito useremo questa semplice regola:  F(x) F(x) = F(b) - F(a) = F(b) - F(a)
come si legge Cioe' prima calcoliamo l'integrale indefinito F(x) poi sostituiamo alla x il valore superiore dell'integrale, mettiamo il segno meno e sostituiamo alla x il valore inferiore dell'integrale. Vediamo un semplice esempio Calcolare l'area della regione di piano limitata dalla curva y = -x2 + 4, e dai semiassi positivi delle x e delle y 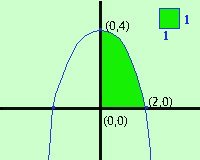
La prima cosa da fare e' costruire la rappresentazione grafica per capire bene come fare: a destra la rappresentazione grafica; l'area da trovare e' quella evidenziata. Siccome l'area sull'asse delle x va da 0 a 2 dovremo calcolare l'integrale:  (-x2+4)dx = (-x2+4)dx =
l'integrale e' immediato e vale - x3 /3 + 4x per indicare che devo fare le differenze uso la notazione
|

|

|

|

|
