Introduzione al calcolo integrale Per capire il perche' del calcolo integrale facciamo un semplice esempio: 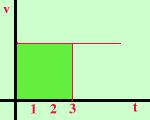Consideriamo il grafico della velocita' rispetto al tempo in un moto rettilineo uniforme Per conoscere lo spazio percorso quando il tempo e' 3 secondi e' sufficiente considerare l'area del rettangolo di colore piu' scuro 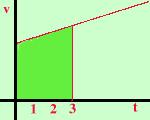Similmente, se il moto fosse uniformemente accelerato, la velocita' varierebbe in modo costante ed il grafico sarebbe quello a sinistra, e lo spazio al tempo 3 sarebbe il trapezio di colore piu' scuro 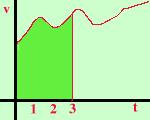Se ora consideriamo un moto con accelerazione variabile il grafico della velocita' diventa una curva e il calcolo dello spazio percorso si riduce a calcolare l'area del "trapezoide"; cosi' viene chiamata la parte di piano compresa fra il grafico e l'asse delle x (in figura la parte piu' scura) Se noi riusciamo a calcolare l'area del trapezoide potremo risalire non solo dalla velocita' allo spazio, ma anche dall'accelerazione alla velocita', dalla forza al lavoro, eccetera; in pratica saremo capaci di fare l'operazione contraria alla derivazione Approfondiamo ora il problema delle aree