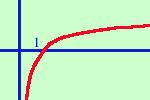
Grafico della funzione logaritmica Dobbiamo distinguere due casi: la base del logaritmo e' maggiore di uno la base dal logaritmo e' compresa fra zero ed uno (in senso lato, cioe' senza gli estremi) la base del logaritmo e' maggiore di uno: allora, qualunque sia la base, y = log x ha le seguenti caratteristiche: la funzione e' sempre crescente e' definita solo per valori positivi della x ha un asintoto verticale nell'asse y in cui la curva tende a - il punto 1,0 e' sempre di intersezione fra la curva e l'asse delle x all'aumentare delle x oltre il punto 1 la curva cresce molto lentamente 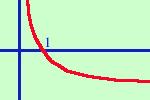la base del logaritmo e' minore di 1 e maggiore di 0: allora, qualunque sia la base in questo intervallo, y = log x ha le seguenti caratteristiche: la funzione e' sempre decrescente e' definita solo per valori positivi della x ha un asintoto verticale nell'asse y in cui la curva tende a + il punto 1,0 e' sempre di intersezione fra la curva e l'asse delle x all'aumentare delle x oltre il punto 1 la curva diminuisce molto lentamente il caso della base minore di zero e' un caso trattato molto raramente, in quanto di solito si lavora con logaritmi a base e; pero' e' sempre meglio essere previdenti...