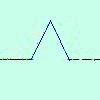
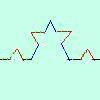
 una funzione continua non e' sempre derivabile,
infatti se ho un punto con un angolo (punto angoloso) non ho la derivata perche' la derivata
destra e' diversa dalla derivata sinistra, inoltre posso pensare curve
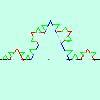
che non hanno nessun punto derivabile: la curva di Peano, la curva di
von Kock. una funzione continua non e' sempre derivabile,
infatti se ho un punto con un angolo (punto angoloso) non ho la derivata perche' la derivata
destra e' diversa dalla derivata sinistra, inoltre posso pensare curve
che non hanno nessun punto derivabile: la curva di Peano, la curva di
von Kock.
Dimostriamo, a completamento della pagina, che se una funzione e' derivabile allora e' anche continua Ho per ipotesi che esiste la derivata finita f '(x0) devo dimostrare che allora la funzione e' continua (tesi) La definizione di continuita' e' che limx->x0 f(x) = f(x0) od anche limh->0 f(x0+h) = f(x0) cioe' limh->0 f(x0+h) - f(x0) = 0 Parto dall'espressione limh->0 f(x0+h) - f(x0) devo dimostrare che vale zero Moltiplico sopra e sotto per h f(x0+h) - f(x0) limh->0 --------------- · h = h la prima parte del prodotto e' la derivata = f '(x0) ·limh->0 h = f '(x0) · 0 = 0 come volevamo dimostrare |

|

|

|

|