 limitato e derivabile all'interno dell'intervallo stesso e se inoltre agli estremi dell'intervallo assume lo stesso valore allora
esiste almeno un punto dell'intervallo in cui la derivata della funzione vale 0.
limitato e derivabile all'interno dell'intervallo stesso e se inoltre agli estremi dell'intervallo assume lo stesso valore allora
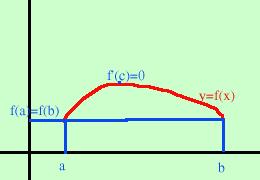
esiste almeno un punto dell'intervallo in cui la derivata della funzione vale 0.come si vede dalla figura in pratica vuol dire che se la funzione parte da un certo valore ed arriva allo stesso valore senza fare punte allora se e' continua e se l'intervallo e' chiuso e limitato ci deve essere un punto dove finisce di crescere (o di diminuire) e torna indietro (si puo' anche dire che la tangente in quel punto e' orizzontale) Matematicamente: se y=f(x) e' una funzione continua in un intervallo chiuso e limitato [a, b] e tale che f(a) = f(b) allora esiste un punto c appartenente ad [a, b] tale che f '(c)=0 L'utilizzo di questo teorema in tante verifiche sia orali che scritte risiede nel fatto che deve verificare quattro ipotesi
capisci che per risolverlo sei costretto a ragionare ed a sapere esattamente cosa si intende per funzione continua, per intervallo chiuso per intervallo limitato eccetera. Dopo aver provato da solo confronta con questi esempi piuttosto alla buona e che non comprendono certo tutti i casi possibili |

|

|

|

|