| Curiosita': storicamente i matematici hanno sempre storto il naso quando hanno visto la loro materia "imbarbarirsi" con altre discipline: fino a pochi decenni fa i geometri hanno guardato dall'alto in basso gli algebristi e questi hanno fatto la stessa cosa con gli studiosi di Analisi;me ne sono reso conto quando frequentavo l'universita' ed una delle discipline che fui costretto a studiare fu la geometria con la riga ed il compasso; pensa che per quasi un secolo dopo la scoperta di Newton e di Leibnitz molti matematici anche italiani rifiutarono l'analisi matematica perche' non "vera" matematica. Fortunatamente oggi, con Godel, Turing e l'avvento dell'informatica parecchi pregiudizi sono spariti Consideriamo un punto che si muova su una traiettoria di moto vario 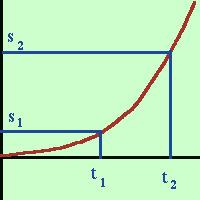 ed il suo
moto sia descrivibile con un'equazione del tipo
ed il suo
moto sia descrivibile con un'equazione del tipoora se voglio la velocita' media nell'intervallo di tempo da t1 a t2 dovro' calcolare il rapporto  s
s2-s1 s
s2-s1----- = -------  t
t2-t1 t
t2-t1 ma questo rapporto, quando prendo un intervallo di tempo molto piccolo mi corrispondera' sia alla derivata dello spazio rispetto al tempo che alla velocita' istantanea v = limt2 ->t1  s/ s/ t =ds/dt= s'(t) t =ds/dt= s'(t)
Quindi per ottenere la velocita' bastera' derivare lo spazio rispetto al tempo Esempio: considero l'equazione del moto uniformemente accelerato con partenza da fermo s = 1/2 a t2 se ne voglio la velocita' sara' sufficiente fare la derivata rispetto alla variabile t v = s'(t) = 1/2 a ·2t = a t che e' la formula per la velocita' nel moto accelerato con partenza da fermo 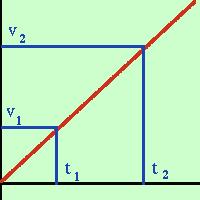 Stesso discorso possiamo fare per l'accelerazione media e l'accelerazione istantanea, in pratica ne deriva che l'accelerazione istantanea e' il limite del rapporto fra la velocita' ed il tempo quando facciamo tendere a zero l'intervallo di tempo cioe' se faccio la derivata della velocita' ottengo l'accelerazione Negli esempi e' riportato il caso del moto uniformemente accelerato con partenza dall'origine e con velocita' iniziale zero In pratica, come forse ho gia' accennato la derivata interverra' in tutte le discipline dove si parlera' di qualcosa che varia al variare di qualcos'altro: ad esempio nei flussi di corrente elettrica o di magnetismo al variare del tempo, nelle variazioni di concentrazione di una soluzione in una reazione chimica, nelle variazioni di popolazione al variare del numero di predatori, eccetera... In tutti i campi della scienza ormai e' necessario conoscere e saper utilizzare le derivate. |

|

|

|

|