Definizione di derivata Dobbiamo vedere come varia la y quando la x varia in modo regolare: intuitivamente il sistema piu' semplice e' quello di considerare un intervallo sulla y ed il corrispondente intervallo sulle x e farne il rapporto: questo mi dara' la variazione media. Se voglio la variazione in un punto dovro' restringere gli intervalli fino a quel punto. Matematicamente: considero sull'asse x i punti 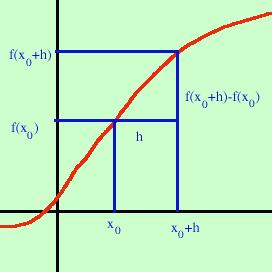x0 e x0+h, in loro corrispondenza avro' i punti f(x0) ed f(x0+h) sull'asse y. La distanza tra f(x0) ed f(x0+h) sull'asse y (in verticale) sara' f(x0+h) - f(x0) mentre la distanza tra x0+h ed x0 sull'asse x sara' x0+h - x0=h chiamiamo rapporto incrementale il rapporto tra la distanza sull'asse y e la distanza sull'asse x:    f(x0+h)- f(x0) -------------------- = rapporto incrementale            h Ora per ottenere la derivata nel punto x0 bastera' far stringere l'intervallo facendo diminuire h                     f(x0+h) - f(x0) limh->0   ----------------- = f'(x0)                            h Definizione: si definisce derivata di una funzione in un punto il limite (se esiste ed e' finito) del rapporto incrementale al tendere a zero dell' incremento h Per avere la derivata generica bastera' considerare il punto come x, cioe' non fisso ma generico sull'asse delle x