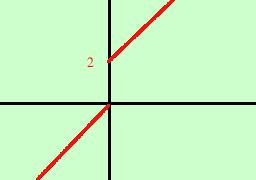
Discontinuita' di prima specie Una discontinuita' si dice di prima specie se esistono finiti i limiti destro e sinistro ma i due limiti sono diversi Esempio: consideriamo la funzione cosi' definita:         x per x <0 y=         x+2 per x 0 essa presenta una discontinuita' di prima specie nel punto zero: infatti: limx->0- f(x) =limx->0- x = 0 limx->0 + f(x)= limx->0 + (x+2) = 2 Attenzione: non e' detto che una funzione debba avere una formula matematica fissa per tutto l'asse reale, io posso definire anche una funzione a pezzi come nell'esempio sopra: l'importante e' che per ogni valore della x corrisponda un solo valore della y un esempio classico di funzione con infiniti punti di discontinuita' di prima specie e' la funzione "scala": 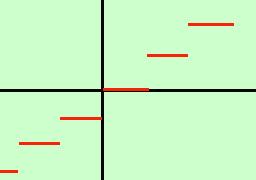      x se x e' un intero y=      int(x) se x non e' intero intendendo con int(x) la parte intera del numero x, cioe' il numero x scritto senza decimali