Primo limite notevole Dobbiamo calcolare il valore del limite: limx->0 senx/x = e per fare questo utilizzeremo il teorema "dei carabinieri", cioe' 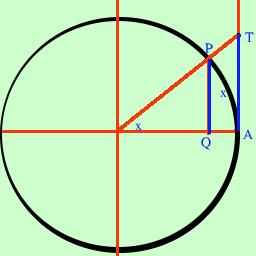prenderemo una funzione che sia sempre maggiore, una funzione che sia sempre minore e vedremo che entrambe le funzioni per x che tende a zero valgono 1 di conseguenza il nostro limite varra' 1 Consideriamo questa disuguaglianza sen x<x<tang x che, come si puo' vedere dalla figura e' valida essendo PQ (sen x) minore dell'arco x che a sua volta e' minore di AT (tang x), ora se divido tutto per senx (e posso farlo senza cambiare niente perche' e' positivo) otterro' sen x/sen x < x/sen x < tang x/sen x semplificando 1 < x/sen x < 1/cos x Ora invertendo i termini basta cambiare di verso alle disuguaglianze 1 > (sen x)/x > cos x ora abbiamo limx->0 1 = 1 e limx->0 cos x = 1 da cio' segue che anche per quella in mezzo limx->0 senx/x = 1