Radici n-esime dell'unita' mediante la formula (in gradi)
x6 = 1
Devo trasformare 1 nella sua forma trigonometrica
trasformazione
1 = cos 0° + i sen 0°
Essendo in campo complesso indico la variabile con w
Devo risolvere l'equazione
w6 = cos 0° + i sen 0°
applico la formula
(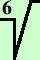 w6
)k+1 = w6
)k+1 =
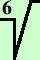 ( (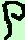 ) ( cos ) ( cos
|
 + k360° + k360°
---------------
6 |
+ i sen |
 + k360° + k360°
---------------
6 |
) |
Con k = 0, 1, 2, 3, 4, 5
 = 0°
e = 0°
e
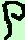 =
1 =
1
ed ottengo:
- per k = 0
( w6
)0+1 = w6
)0+1 =
 1 (
cos 1 (
cos
|
0° + 0·360°
---------------
6 |
+ i sen |
0° + 0·360°
---------------
6 |
|
w1 =
cos
|
0°
----
6 |
+ i sen |
0°
---- =
6 |
= cos 0° + i sen 0° = 1 + i0 = 1
- per k = 1
( w6
)1+1 = w6
)1+1 =
 1 (
cos 1 (
cos
|
0° + 1·360°
---------------
6 |
+ i sen |
0° + 1·360°
---------------
6 |
|
w2 =
cos
|
360°
-------
6 |
+ i sen |
360°
------- =
6 |
= cos 60° + i sen 60° =
= 1/2 + i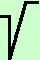 3 /2 = 3 /2 = |
1 + i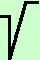 3 3
--------
2 |
- per k = 2
( w6
)2+1 = w6
)2+1 =
 1 (
cos 1 (
cos
|
0° + 2·360°
---------------
6 |
+ i sen |
0° + 2·360°
---------------
6 |
) |
|
w3 =
cos
|
720°
-------
6 |
+ i sen |
720°
------- =
6 |
= cos 120° + i sen 120° =
= -1/2 + i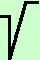 3 /2 = 3 /2 = |
-1 + i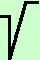 3 3
--------
2 |
- per k = 3
( w6
)3+1 = w6
)3+1 =
 1 (
cos 1 (
cos
|
0° + 3·360°
---------------
6 |
+ i sen |
0° + 3·360°
---------------
6 |
) |
|
w4 =
cos
|
1080°
-------
6 |
+ i sen |
1080°
------- =
6 |
= cos 180° + i sen 180° =
-1 + i·0 = -1
- per k = 4
( w6
)4+1 = w6
)4+1 =
 1 (
cos 1 (
cos
|
0° + 4·360°
---------------
6 |
+ i sen |
0° + 4·360°
---------------
6 |
) |
|
w5 =
cos
|
1440°
-------
6 |
+ i sen |
1440°
------- =
6 |
= cos 240° + i sen 240° =
= -1/2 - i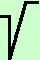 3 /2 = 3 /2 = |
-1 - i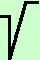 3 3
--------
2 |
- per k = 5
( w6
)5+1 = w6
)5+1 =
 1 (
cos 1 (
cos
|
0° + 5·360°
---------------
6 |
+ i sen |
0° + 5·360°
---------------
6 |
) |
|
w6 =
cos
|
1800°
-------
6 |
+ i sen |
1800°
------- =
6 |
= cos 300° + i sen 300° =
= 1/2 - i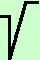 3 /2 = 3 /2 = |
1 - i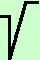 3 3
--------
2 |
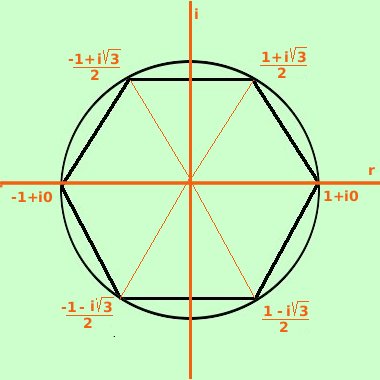
quindi, raccogliendo abbiamo
l'ordine e' diverso da quello
delle soluzioni trovate con il metodo algebrico: nota che il metodo della
formula ti da' le soluzioni ordinate in senso antiorario sulla
circonferenza
 w1 = 1
w1 = 1
| w2 = |
1 + i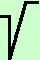 3 3
--------
2 |
| w3 = |
-1 + i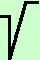 3 3
--------
2 |
w4 = -1
| w5 = |
-1 - i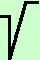 3 3
--------
2 |
| w6 = |
1 - i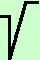 3 3
--------
2 |
|
 w1 = 1
w1 = 1