Radici n-esime dell'unita' mediante la scomposizione di polinomi Purtroppo questo metodo non e' sempre applicabile, ad esempio non potrai applicarlo alle equazioni x5=1 , x7=1,... Puoi applicarlo solamente quando puoi scomporre in modo che i polinomi componenti siano di grado 1 e 2 (sarebbe possibile anche con i polinomi di terzo grado, ma la formula risolutiva delle equazioni associate a tali polinomi non sono trattate nelle scuole medie superiori) x6 = 1 Equivale a x6 - 1 = 0 scompongo secondo il metodo polinomiale (differenza di quadrati prima e poi differenza e somma di cubi) il termine prima dell'uguale x6-1 = (x3-1)(x3+1)= (x-1)(x2+x+1)(x+1)(x2-x+1) ottengo x6-1 = (x3-1)(x3+1)= (x-1)(x2+x+1)(x+1)(x2-x+1)=0 cioe' devo risolvere le equazioni x - 1 = 0 x2 + x + 1 = 0 x + 1 = 0 x2 - x + 1 = 0 Risolvo la prima e trovo la prima soluzione x - 1 = 0 x1 = 1 cioe' nel campo complesso x = 1 + i0 Risolvo la seconda e trovo la seconda e la terza soluzione x2 + x + 1 = 0 e' un'equazione di secondo grado, la risolvo e trovo x2 =   -1 + i3 -------- 2       x3 =   -1 - i3 -------- 2        Calcoli Risolvo la terza equazione e trovo la quarta soluzione x + 1 = 0 x4 = -1 cioe' nel campo complesso x = -1 + i0 Risolvo la quarta e trovo la quinta e la sesta soluzione x2 - x + 1 = 0 e' un'equazione di secondo grado, la risolvo e trovo x2 =   1 + i3 -------- 2       x3 =   1 - i3 -------- 2        Calcoli Raccogliendo. le soluzioni in campo complesso sono: le indico con i simboli w1, w2, w3,..... 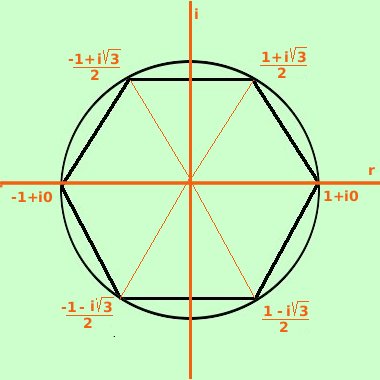w1 = 1 + i0 w2 =   1 + i3 -------- 2 w3 =   1 - i3 -------- 2 w4 = -1 + i0 w5 =   -1 + i3 -------- 2 w6 =   -1 - i3 -------- 2