|
Finora i numeri sono come dei paracarri su una stada, cioe' sono a distanza regolare fra loro ma in mezzo fra un numero e l'altro non c'e' niente, quindi, per poter sempre fare la divisione dovro' riempire questi spazi indicando ognuno col suo nome i valori che posso trovare. Il problema e': come fare? Il sistema piu' semplice e' quello di indicare il punto mediante il valore della divisione: cioe' il punto che otterrei considerando la divisione lo chiamero' semplicemente + -- 2 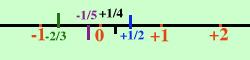 esistente fra i numeri interi degli infiniti
risultati che otterrei eseguendo le possibili divisioni fra numeri
interi:
esistente fra i numeri interi degli infiniti
risultati che otterrei eseguendo le possibili divisioni fra numeri
interi:1/1, 1/2, 1/3, 1/4, 1/5, ..... 2/1, 2/2, 2/3, 2/4, 2/5, ..... 3/1, 3/2, 3/3, 3/4, 3/5, ..... .................................... per approfondire C'e' da dire che esiste un numero che fa eccezione: lo zero! infatti non posso dividere per zero, quindi non hanno significato i numeri 1/0, 2/0, 3/0, 4/0,... Indichero' con Q (insieme dei numeri razionali) questo nuovo insieme |

|

|

|

|