Risolvere la seguente equazione logaritmica log2(x+1) = log4(2x+5) Siccome il logaritmo e' definito solamente se l'argomento e' maggiore di zero dovremo risolvere l'equazione sotto le condizioni: x + 1 > 0 2x + 5 > 0 risolvo x > -1 x > -5/2 Essendo un sistema devo prendere l'intervallo dove sono valide contemporaneamente le disequazioni cioe' 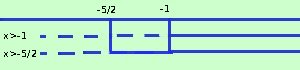x > -1 Adesso passo a risolvere l'equazione log2(x+1) = log4(2x+5) Siccome i logaritmi hanno base diversa dovro' applicare la regola del cambiamento di base. Conviene trasformare il secondo logaritmo da base 4 in base 2 Applico la regola log2(2x+5) log2(2x+5) log4(2x+5) = ---------------- = ---------------- log24 2 quindi posso scrivere log2(x+1) = 1/2log2(2x+5) e ricordando la regola del logaritmo di un radicale log2(x+1) = log2(2x+5) cioe', uguagliando gli argomenti (x+1) = (2x+5) E' un'equazione irrazionale: elevo al quadrato da entrambe le parti (x+1)2 = 2x+5 sviluppo il quadrato x2 + 2x + 1 = 2x+5 x2 + 2x + 1 - 2x - 5 = 0 x2 - 4 = 0 x2 = 4 x = 4 ottengo le soluzioni x = 2          x = -2 Per l'equazione irrazionale dovrei vedere se le soluzioni sono accettabili, pero' ho visto sempre che corrisponde all'accettabilita' della soluzione dell'equazione logaritmica Per l'equazione logaritmica controllo che le soluzioni siano conprese nell'intervallo di definizione x >-1 La soluzione x = 2 e' accettabile perche' maggiore di -1 La soluzione x = -2 non e' accettabile perche' minore di -1