Risolvere la seguente equazione logaritmica log(x+1) + log(x-1) = 0 Siccome il logaritmo e' definito solamente se l'argomento e' maggiore di zero dovremo risolvere l'equazione sotto le condizioni: x + 1 > 0 x - 1 > 0 risolvo x > -1 x > 1 Essendo un sistema devo prendere l'intervallo dove sono valide contemporaneamente le disequazioni cioe' 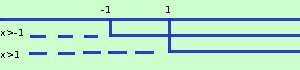x > 1 Adesso passo a risolvere l'equazione log(x+1) + log(x-1) = 0 Per la regola del logaritmo di un prodotto posso scrivere log (x-1)(x+1) = 0 calcolo prima dell'uguale e, ricordando che zero e' il logaritmo di 1 log (x2-1) = log 1 cioe', uguagliando gli argomenti x2-1 = 1 x2 = 2 x = 2 Ora devo controllare se le soluzioni cadono nell'intervallo di definizione: la soluzione x = -2 e' esterna all'intervallo di definizione perche' e' minore di 1 e quindi non e' accettabile la soluzione x = +2 e' interna all'intervallo di definizione perche' e' maggiore di 1 e quindi e' accettabile cioe' x = +2 e' accettabile