Risolvere la seguente equazione logaritmica log(x-2) - log(x-3) = log 4 Siccome il logaritmo e' definito solamente se l'argomento e' maggiore di zero dovremo risolvere l'equazione sotto le condizioni: x - 2 > 0 x - 3 > 0 risolvo x > 2 x > 3 Essendo un sistema devo prendere l'intervallo dove sono valide contemporaneamente le disequazioni cioe' 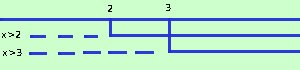x > 3 Adesso passo a risolvere l'equazione log(x-2) - log(x-3) = log 4 Per la regola del logaritmo di un quoziente posso scrivere x - 2 log -------- = log 4 x - 3 cioe', uguagliando gli argomenti x - 2 -------- = 4 x - 3 Supponendo x diverso da 3 (sovrabbondante perche' x = 3 era gia' escluso dalle condizioni iniziali) faccio il m.c.m. x - 2 4(x - 3) -------- = ----------------   x - 3 x - 3 tolgo i denominatori x - 2 = 4(x - 3) calcolo x - 2 = 4x - 12 x - 4x = 2 - 12 -3x = -10 x = 10/3 Ora devo controllare che la soluzione cada nell'intervallo di definizione: 10/3 e' maggiore di 3 quindi la soluzione 10 x = ---- 3 e' accettabile In qualche scuola ho visto anche risolverlo con un sistema in questo modo: x - 2 > 0 x - 3 > 0 log(x-2) - log(x-3) = log 4 Formalmente e' piu' giusto ma come svolgimento e' la stessa cosa